🔗 백준 1010 문제 https://www.acmicpc.net/problem/1010
문제
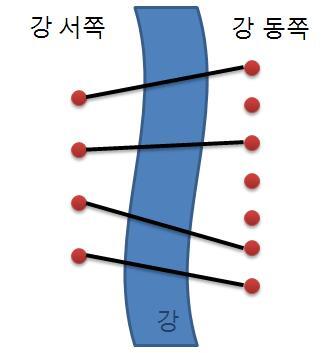
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)
재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.
입력
입력과 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트 케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N <= M < 30) 이 주어진다.
출력
각 테스트 케이스에 대해 주어진 조건 하에 다리를 지을 수 있는 경우의 수를 출력한다.
풀이
일단 이 문제를 딱 봤을때 든 경우의 수와 중복이 허락되지 않는다는 부분에서 조합을 떠올렸다.
조합
n 개의 원소 중 순서를 고려하지 않는 경우의 수. 즉, 중복을 제거한 순열이라고 볼 수 있다.
nCr = n−₁Cr−₁ + n−₁Cr
조합은 위와 같은 공식을 갖고 있는데 이는,
하나의 원소를 선택할 경우 + 하나의 원소를 선택하지 않을 경우로 나타낼 수 있다.
예를 들면 [1, 2, 3, 4, 5] 가 있을 때 3개를 뽑는 경우를 구한다고 하면
- 5를 미리 선택할 경우 : 남은 수 [1, 2, 3, 4]. 선택된 수 [5]
- 남은 수 중 2개를 선택할 수 있는 경우 = [1, 2, 5], [1, 3, 5], [1, 4, 5], [2, 3, 5], [2, 4, 5], [3, 4, 5]. 총 6개
- 5를 선택하지 않을 경우 : 남은 수 [1, 2, 3, 4]
- 남은 수 중 3개를 선택할 수 있는 경우 = [1, 2, 3], [1, 2, 4], [1, 3, 4], [2, 3, 4]. 총 4개
즉, 5Cr = 4C2 + 4C3 = 10개가 된다.
뽑아야 할 개수인 r이 0이 되면 선택의 여지가 없으므로 1을 리턴시킨다.
전체 개수와 뽑아야 할 개수가 같다면 이 또한 선택의 여지가 없으므로 1을 리턴시킨다.
그리고 0.5 초라는 시간 제한이 있기에 Dynamic Programming 알고리즘 기법의 Top-down 을 활용하여 수행 시간 효율성을 향상시켜주었다.
동적 계획법 Dynamic Programming
DP 알고리즘 기법은 이미 계산된 결과를 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 설계하여 수행 시간 효율성을 향상시키는 방법이다.
Top-down 하향식
상위 문제 해결을 위해 하위 문제를 재귀로 호출하여 하위 문제부터 상위 문제까지 순차적으로 해결하는 방식. 해결해놓은 하위 문제를 저장하기 위해 Memoization이 사용된다.
Memoization
한번 계산한 결과를 메모리 공간에 메모하는 기법.
메모이제이션 사용을 통해 모든 문제가 단 한번씩만 계산된다고 보장되기에 함수 호출 횟수가 감소된다.
내가 푼 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
private static final int[][] dp = new int[30][30]; // 메모이제이션 위한 행렬, 구한 값을 바로 저장해둔다
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
for (int i = 0; i < T; i++) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
bw.write(recursive(M, N) + "\n");
}
bw.flush();
bw.close();
}
// M 에서 N을 뽑는 경우의 수
private static int recursive(int n, int r) {
/**
* 메모이제이션 O(n)
* 한번 구한 값은 저장된 값 리턴
*/
if (dp[n][r] > 0) {
return dp[n][r];
}
else if (n == r || r == 0) {
return dp[n][r] = 1;
}
else {
/**
* Combination 조합
* nCr = n-1Cr-1 + n-1Cr
* (n-1Cr-1) : 하나의 원소를 선택할 경우
* (n-1Cr) : 하나의 원소를 선택하지 않을 경우
*/
return dp[n][r] = recursive(n - 1, r - 1) + recursive(n - 1, r);
}
}
}
참고 블로그
https://woongsios.tistory.com/179
https://loosie.tistory.com/150
'Algorithm' 카테고리의 다른 글
| [BaekJoon] 1181 단어 정렬 JAVA (0) | 2022.12.23 |
|---|---|
| [BaekJoon] 1064 평행사변형 JAVA (1) | 2022.12.21 |
| [BaekJoon] 2034 반음 JAVA (0) | 2022.12.21 |
| [BaekJoon] 1542 세준세비 JAVA (0) | 2022.12.20 |
| [BaekJoon] 1032 명령프롬프트 JAVA (0) | 2022.12.20 |



